When I first began my career in 1989 (yes that was pre-internet for those of you youngsters out there!), part of my training in mathematics was on the CRA approach: Concrete Representational Abstract. Jerome Bruner, a 1960’s American psychologist, believed that the nature of abstract learning was a ‘mystery’ to many children. He found that when students engaged in the progressional stages of CRA, they could build on each stage toward a greater understanding of complex mathematical concepts. Let’s talk about the CRA method!
“CRA is a sequential instructional approach during which students move from working with concrete materials to creating representational drawings to using abstract symbols. Using this concrete-representational-abstract sequence helps students develop the thorough mental representations that are foundational for conceptual understanding.” Source: Digital Promise
So what is CRA, and how does it work? Think about the way we approach literacy with our students. Reading is a complex task, and in order for children to understand what a word is, they must have seen it first (concrete). The letters (representational) b-a-t only have meaning when we know what a bat looks like. The word brings the visual of either a baseball bat or an animal. It is only with context (abstract) that we can begin to distinguish which visual makes the most sense for what we are reading.
Now…let’s translate to math. When young children begin to count to 5, they will do so by memorizing the numbers. They won’t have a true understanding of what the value of 5 means, as this requires abstract understanding. As they move on to playing with blocks (concrete), they will begin understanding that when they have three blocks and they count them out loud, they stop at the number 3. Once they have practice with this 1:1 correspondence, they can move on to understanding that the written numeral 5 (representational) is equal to five of something.
This is what makes Cube and Glow perfectly aligned to the instructional scaffolding of CRA. The cubes (Cube) and dials (Glow) allow for students to engage with the concrete manipulatives needed to explore complex mathematical concepts. They also provide representational diagrams of tens blocks (Cube) or arrays (Glow) so that students can make the necessary connections between the concrete and representational. Last but not least, it provides students with the number sentences and equations that represent the abstract thinking needed to become fluent in number sense and problem solving.
For example, the following complex task is outlined on the screen below. It is from Cube’s ‘Hundreds’ and ‘Build.’
In order to solve this problem, students will engage with concrete manipulatives by placing cubes within the correct place value column.
As students move between the concrete and representational phases, they will first count the number of physical objects they used to create the number; in this case 16 cubes were used. The number 286 represents a number that is between the value of 100 and 300. The abstract concept that students should eventually realize is that the value of the numbers in this case (2 + 8 + 6 = 16), is the same as the number of cubes used to represent the number. There are two groups of 100, eight groups of 10, and six of 1. This is the foundation for understanding place value.
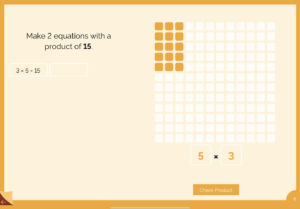
When using Glow’s ‘Multiplication’ and ‘Make’ mode, students will engage with the concrete (kinesthetic) by using the dials on Glow to create a variety of arrays that represent a given product (in the example below a product of 15). As students move from concrete to representational they will move from counting the squares individually to skip counting by fives or maybe threes. These are essential skills to understanding the abstract concept that 3 x 5 = 15. This mode also introduces the concept of the commutative property of multiplication in that 3 x 5 = 5 x 3.
I was part of a pilot group working with 4th grade students on multiplication, and while using Glow, students were thoroughly engaged! By pulling them into small groups of five, I could easily see how students were moving between the concrete and representational by observing which students were counting out squares, which ones were skip counting, which had memorized the multiplication table, and which had true understanding of the array and how it related to the product.
As you can see, Cube and Glow can help teachers understand mathematical thinking in action! Not only can we see the students working with manipulatives (concrete), but the ways in which they interact with the on screen representations can give us insight into their abstract thinking. Stay tuned… as the next three posts will focus on breaking down each aspect of CRA and how it can be applied to specific modules within the Owlet products!
- Concrete
- Representational
- Abstract
Heidi Williams is the Computer Science Curriculum Specialist for Marquette University in Milwaukee, WI. Her focus is on the K-8 integration of computer science and computational thinking within all core content areas. She is the author of ISTE’s No Fear Coding: Computational Thinking Across the K-5 Curriculum, as well as a facilitator of ISTE-U’s Computational Thinking for Every Educator course.
Within this Blog, Heidi will be posting on how Cube and Glow can help educators to support their students’ mathematical thinking. Over the course of the next three months, you will hear about best practices in pedagogical use, CRA – concrete, representational, abstract connections, visualization of partial products, connections to mathematical standards, and MUCH more!
Within each post you will find detailed explanations, links directly back to the components and resources of Cube and Glow, as well as external links that will provide you with more background information and support in teaching a variety of mathematical standards. As you continue to read her posts, week after week, we hope you fall in love with Cube and Glow. We also hope you enjoy the wealth of mathematical pedagogical content and strategies she shares.
Heidi has an extensive background in mathematical pedagogy, with over fifteen years of experience as a 6th – 8th grade math teacher, as well as a K-8 mathematics specialist. She has had extensive training in differentiation, coaching within a Response to Intervention (RtI) framework, as well as inquiry based instruction. Birdbrain is tapping into her understanding and passion for helping K-8 teachers with mathematical thinking in the classroom. Please join us and follow Heidi’s Hoots!