While Glow and Cube are not necessarily focused on computer science standards, the philosophy of the developers is founded on the K-12 framework. “As illustrated in Figure 1.1, the framework provides building blocks of concepts (that students should know) and practices (that students should do) which can be used to create standards (performance expectations of what students should know and do).”
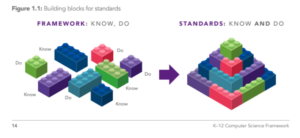
This foundation uses the analogy of concrete lego blocks. As you can see from the diagram, the framework is built upon things that students know and can do. When you put them together (snap the blocks together) you have standards. This can be applied to both computer science and mathematics. We need students to ‘do’ something to show their knowledge. The more concrete the structures in the beginning, the more we (as educators) can see where the students are in their thinking. Once a base layer of knowledge is solidified, then we can keep building upwards. If the foundation is not solid, the skills that come later will be unstable and the structure could tumble apart.
Cube and Glow have concrete tools that will help students show their thinking in representational and abstract ways. Cube uses cubes, and it comes with a bag of 30 cubes that can be easily stored when not in use. Glow uses two dials, a right and a left, that can be turned to demonstrate rows and columns (arrays) on the screen. The concrete manipulation of cubes and dials allows students to engage in the concrete thinking that eventually leads to representations.
Cube can be used in teaching CCSS: 2.MD.C.8 – solve word problems involving dollar bills, quarters, dimes, nickels, and pennies, using $ and ¢ symbols appropriately. For example, when working with ‘Money’ on ‘Build’ the word problem appears on the app and students can either read it or click on the speaker icon to have the problem read to them. In this case, it states: “Compose a number between $2.80 and $4.60 with 18 cubes.” 
Students will usually tackle this problem one of two ways: They will either begin placing blocks in the $0.01 column, or they will begin placing them in the dollar ($1) column. Let’s start by digging into the $0.01 column first. Students will usually place as many blocks in this column as they can. If they place 9 blocks here, that gives them 9 blocks left to use. Since the dollar amount needs to be between $2 and $4, they will usually place 3 blocks in the dollar column. This leaves 6 blocks left for the $0.10 column. Their final amount = $3.69.
For the example in the diagram above, students began placing 3 blocks in the dollar column, since the value had to be between $2 and $4 dollars. They then placed as many blocks as they could in the $0.10 column, which ends up being 9 blocks. Lastly, they place the remaining 6 blocks in the $0.01 column. Their final amount = $3.96. When working with money, both methods produce the same efficiency.
Now, let’s look at Glow. Glow can be used in teaching CCSS: 2.NBT.C.7– add and subtract within 1000, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.For example, when working with ‘Addition’ on Level 5 in ‘Find’ mode, students are first asked to find the missing value for _____ + 22 = 120. They use the concrete dial on the left to input the number 22, which lights up the blue lights. Students will discover that the last two columns of the Glow Grid do not light up, which makes for a grid that has rows of ten dots. This makes it easier to count, and teachers can refer back to our base ten number system to explain why.
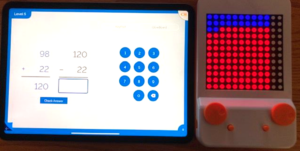Students then need to determine how many dots they need to turn red in order to = 120. Depending on the students’ mathematical number sense, they may tackle the task in the following ways:
- Start with 22 and then count the red dots individually until = 120. Then go back and count the number of red dots individually.
- Start with 22 and then add 8 more = 30. Then continue counting on until 120. Once finished, count the red dots by 10’s and add 8 more to = 98.
- Count the 8 red dots and then continue counting by increasing the number +10 (18, 28, 38, etc…) until they reach the number 98.
Watching this as the teacher, it will provide a wealth of information as to a student’s number sense. The first example shows 1:1 correspondence only; the student is not yet making groups of ten. The second example shows the ability to work with groups of ten, but is lacking in efficiency, as the student will need to go back and re-count to obtain the missing number. The third example demonstrates efficiency, as the student will arrive at the final answer.
Glow also makes the relationship between addition and subtraction stand out visually. WIth addition, the blue + red = total lights lit. With subtraction, the total lights lit – red = blue, and the total lights lit – blue = red. This touches on the commutative property as well.
As you can see, both Cube and Glow help students to engage physically, with concrete manipulatives, to help show mathematical concepts in a representational way. Watching how students use these tools will provide you with insight into how they think! Stay tuned in our next post, as I will dive deeper into the representations that Cube and Glow can help our students develop!
Get caught up on all of Heidi’s Hoots:
WELCOME TO HEIDI’S HOOTS
FULL CLASS EXPLORATION WITH OWLET
INDEPENDENT MATH CENTERS WITH OWLET
SMALL GROUP MATH TALK WITH OWLET
CONCRETE, REPRESENTATIONAL, AND ABSTRACT THINKING IN ACTION
Heidi Williams is the Computer Science Curriculum Specialist for Marquette University in Milwaukee, WI. Her focus is on the K-8 integration of computer science and computational thinking within all core content areas. She is the author of ISTE’s No Fear Coding: Computational Thinking Across the K-5 Curriculum, as well as a facilitator of ISTE-U’s Computational Thinking for Every Educator course.
Within this Blog, Heidi will be posting on how Cube and Glow can help educators to support their students’ mathematical thinking. Over the course of the next three months, you will hear about best practices in pedagogical use, CRA – concrete, representational, abstract connections, visualization of partial products, connections to mathematical standards, and MUCH more!
Within each post you will find detailed explanations, links directly back to the components and resources of Cube and Glow, as well as external links that will provide you with more background information and support in teaching a variety of mathematical standards. As you continue to read her posts, week after week, we hope you fall in love with Cube and Glow. We also hope you enjoy the wealth of mathematical pedagogical content and strategies she shares.
Heidi has an extensive background in mathematical pedagogy, with over fifteen years of experience as a 6th – 8th grade math teacher, as well as a K-8 mathematics specialist. She has had extensive training in differentiation, coaching within a Response to Intervention (RtI) framework, as well as inquiry based instruction. Birdbrain is tapping into her understanding and passion for helping K-8 teachers with mathematical thinking in the classroom. Please join us and follow Heidi’s Hoots!